Les révisions mathématiques des concepts essentiels du collège : votre guide complet
Les mathématiques au collège posent-elles des difficultés à votre enfant ? Selon les derniers chiffres du ministère de l’Éducation nationale (2024), 38% des élèves éprouvent des difficultés avec les concepts géométriques fondamentaux. Une révision méthodique permet pourtant de consolider durablement ces acquis essentiels. Maîtriser les bases comme comprendre le théorème de Pythagore devient alors accessible avec une approche progressive et structurée.
Pourquoi ces notions fondamentales déterminent votre réussite au brevet
Les mathématiques au collège forment une chaîne de connaissances où chaque notion s’appuie sur les précédentes. Le théorème de Pythagore en quatrième devient ainsi la clé pour résoudre des problèmes de géométrie plus complexes en troisième, puis pour réussir l’épreuve du brevet.
A lire en complément : Découvrir les Stratégies Innovantes de Formation Internationale pour Entreprises
Cette progression logique explique pourquoi certains élèves peinent dans les classes supérieures. Une lacune sur les propriétés des triangles rectangles compromet la compréhension des fonctions trigonométriques. C’est exactement ce que nous observons lors de nos accompagnements : les difficultés actuelles résultent souvent de bases mal consolidées.
Au-delà du cadre scolaire, ces compétences mathématiques développent un raisonnement rigoureux. Calculer des distances, évaluer des surfaces ou résoudre des problèmes concrets devient naturel. Notre approche pédagogique privilégie d’ailleurs ces applications pratiques pour donner du sens aux apprentissages.
A voir aussi : Les pièges fatals du e-commerce : l’importance cruciale de la formation
La maîtrise de ces fondamentaux représente donc bien plus qu’une simple préparation au brevet : elle constitue un socle durable pour la réussite mathématique future.
Méthode d’apprentissage progressive du théorème de Pythagore
L’apprentissage du théorème de Pythagore nécessite une approche structurée pour éviter les confusions. Cette méthode progressive permet aux élèves d’assimiler les concepts étape par étape, depuis les bases jusqu’aux applications complexes.
- Révision des prérequis : maîtrise des carrés, racines carrées et reconnaissance des triangles rectangles avec identification de l’hypoténuse
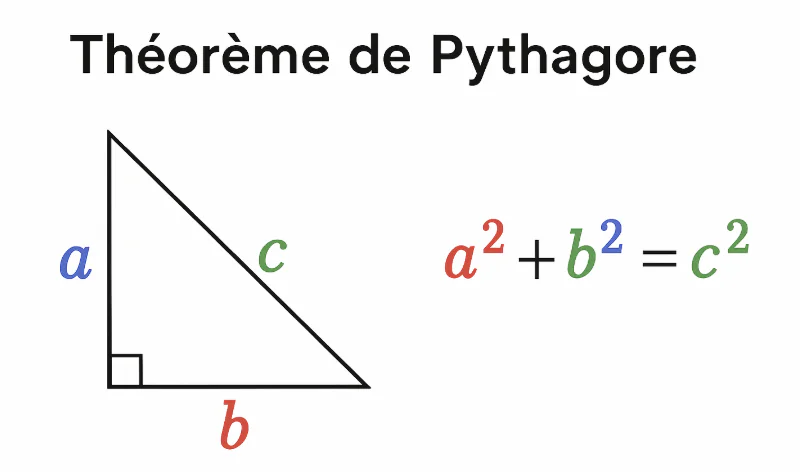
- Apprentissage de la formule : mémorisation de a² + b² = c² avec compréhension du rôle de chaque variable dans la relation
- Applications directes : calculs simples d’hypoténuse avec des valeurs entières pour consolider la compréhension
- Applications inverses : détermination des côtés de l’angle droit et vérification qu’un triangle est rectangle
- Vérifications systématiques : contrôle de la cohérence des résultats et identification des erreurs de calcul courantes
Cette progression méthodique garantit une compréhension solide du théorème. Les élèves développent progressivement leur autonomie dans la résolution de problèmes géométriques variés.
Applications pratiques et exemples concrets au quotidien
Le théorème de Pythagore ne reste pas enfermé dans les manuels scolaires ! Les architectes l’utilisent quotidiennement pour vérifier que les angles de leurs constructions sont parfaitement droits. Ils mesurent trois longueurs sur un terrain et appliquent la formule a² + b² = c² pour s’assurer de la précision géométrique de leurs fondations.
Dans le domaine sportif, les entraîneurs de football calculent les distances de courses en diagonale sur le terrain. Un joueur qui court de son but vers le corner opposé parcourt exactement √(100² + 70²) = 122 mètres, soit bien plus que les dimensions apparentes du terrain.
Les exemples d’exercices concrets permettent de maîtriser ces calculs. Imaginez une échelle de 5 mètres appuyée contre un mur, avec sa base à 3 mètres du mur. Sa hauteur d’appui se calcule simplement : √(5² – 3²) = 4 mètres. Cette méthode de calcul pratique s’avère indispensable pour tous les métiers du bâtiment et de l’aménagement.
Comment éviter les erreurs courantes des élèves
Les collégiens font souvent les mêmes erreurs avec le théorème de Pythagore. La plus fréquente consiste à confondre les côtés avec l’hypoténuse lors de l’application de la formule. Cette confusion vient généralement d’une mauvaise identification du triangle rectangle et de ses éléments.
Pour éviter cette erreur, pensez à cette astuce simple : l’hypoténuse est toujours le côté le plus long, celui qui se trouve en face de l’angle droit. Tracez mentalement ou au crayon l’angle droit avant de commencer vos calculs. Cette vérification préalable vous évitera bien des déconvenues.
Les erreurs de calcul représentent également un piège classique. Vérifiez toujours vos résultats en appliquant la méthode inverse : si vous avez trouvé l’hypoténuse, recalculez un des autres côtés pour valider votre réponse. Cette double vérification permet de détecter les erreurs arithmétiques.
Enfin, méfiez-vous des triangles qui « semblent » rectangles sur le dessin. Sans indication claire sur l’angle droit, vous pourriez appliquer le théorème de Pythagore à tort. Cherchez toujours le petit carré qui matérialise l’angle de 90 degrés.
Stratégies de révision efficaces pour le brevet des collèges
La préparation du brevet en mathématiques nécessite une planification méthodique sur plusieurs mois. Commencez vos révisions dès janvier pour couvrir sereinement l’ensemble du programme de 4ème et 3ème. Consacrez 30 minutes quotidiennes aux mathématiques plutôt que des sessions intensives ponctuelles.
Les annales des années précédentes constituent votre meilleure ressource d’entraînement. Elles vous familiarisent avec les types d’exercices récurrents et le niveau d’exigence attendu. Complétez avec des manuels scolaires et des plateformes numériques offrant des exercices interactifs adaptés.
Pour mémoriser durablement les formules et théorèmes, utilisez la technique des fiches synthétiques. Rédigez les propriétés essentielles avec des schémas colorés. Testez-vous régulièrement sans regarder vos notes, puis vérifiez immédiatement vos réponses.
La correction personnalisée reste cruciale pour progresser efficacement. Analysez chaque erreur pour comprendre l’origine du problème : incompréhension du cours, erreur de calcul ou mauvaise interprétation de l’énoncé. Cette démarche vous évitera de reproduire les mêmes fautes le jour J.
Vos questions sur le théorème de Pythagore
Comment réviser le théorème de Pythagore pour le brevet ?
Maîtrisez d’abord la formule de base : a² + b² = c². Entraînez-vous avec des exercices variés, identifiez l’hypoténuse et vérifiez toujours vos calculs. Révisez également la réciproque pour déterminer si un triangle est rectangle.
Quels sont les concepts mathématiques essentiels à connaître en 4ème et 3ème ?
Le théorème de Pythagore et sa réciproque, les équations du second degré, la trigonométrie, les fonctions linéaires et affines, ainsi que les statistiques et probabilités. Ces bases sont cruciales pour réussir le brevet.
Comment calculer l’hypoténuse d’un triangle rectangle facilement ?
Identifiez les deux côtés de l’angle droit, élevez-les au carré, additionnez-les puis calculez la racine carrée du résultat. Exemple : côtés 3 et 4, alors hypoténuse = √(9 + 16) = 5.
Quelles sont les erreurs à éviter avec le théorème de Pythagore ?
Ne confondez jamais l’hypoténuse avec un autre côté. Vérifiez que le triangle est bien rectangle. Attention aux calculs de racines et n’oubliez pas d’arrondir selon les consignes données.
Comment savoir si un triangle est rectangle avec le théorème de Pythagore ?
Utilisez la réciproque : calculez le carré du plus grand côté et comparez-le à la somme des carrés des deux autres. Si l’égalité est vérifiée, le triangle est rectangle.
